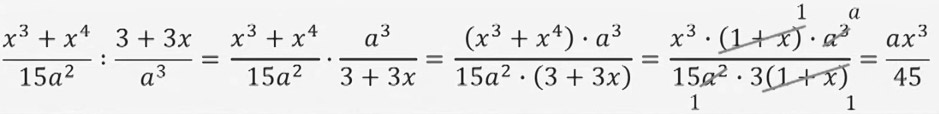Рационалдык туюнтмалар

Рационалдык туюнтма деп - сандардан, өзгөрүлмөлөрдөн, алардын даражаларынан арифметикалык амалдардын белгилеринен турган туюнтманы аташат.

• 5ab
• x² + 2xy + y²
• 

Рационалдуу туюнтма бүтүн жана бөлчөктүү туюнтмадан турат.

Бүтүн туюнтма

Нөлдөн айырмаланган өзгөрмөлүү туюнтмаларга кошуу, кемитүү, көбөйтүү жана бөлүү амалдарынын жардамы менен сандардан жана өзгөрмөлөрдөн түзүлгөн туюнтма - бүтүн туюнтма болот.

• 2xy²z
• (x+y)(a²-xc³):7
• 

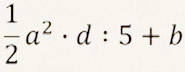
Каалагандай бүтүн туюнтманы көп мүчө түрүндө көрсөтүүгө болот.

Бөлчөктүү туюнтма

Өзгөрмөлүү туюнтмаларга кошуу, кемитүү, көбөйтүү жана бөлүү амалдарынын жардамы менен сандардан жана өзгөрмөлөрдөн түзүлгөн туюнтма - бөлчөктүү туюнтма болот.

• 
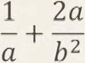
• z-5xy:z²
• 

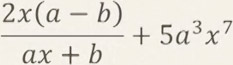
Туюнтмалардын аныкталуу областы

Туюнтма кайдайдыр бир чыныгы маанигэ ээ болгон өзгөрмөлөрдүн маанисин өзгөрмөлөрдүн мүмкүн болгон маанилери деп аташат.

Өзгөрмөлөрдүн мүмкүн болгон бардык маанилеринин көптүгүн өзгөрмөнүн мүмкүн болгон маанилеринин областы же туюнтманын аныкталуу областы деп айтышат.

Бүтүн туюнтманын аныкталуу областы - өзгөрмөнүн бардык маанилери.

ax² : 5 + 3p⁴z бүтүн туюнтмасы a, x, p жана z бардык чыныгы маанилеринде мааниге ээ болот.

Бөлчөк туюнтманын аныкталуу областы - бул туюнтманын бөлүүчүлөрүнүн нөлгө барабар болбогон өзгөрүлмөлөрдүн бардык маанилери болот.

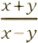бөлчөктүү туюнтмасы x = y болгондо мааниге ээ болбойт.

Рационалдык туюнтманын маанисин табу үчүн эмне керек:

1. Берилген туюнтманын өзгөрүлмөлөрүнүн ордуна сандык маанилерин коюуу;
2. Бардык амалдарды аткаруу.

Бөлчөктүн маанисин табуу

Эгер 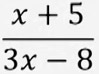бөлчөк берилип "X"тин мааниси 10го барабар болсо (x=10), анда бөлчөктөгү Xтердин ордуна 10 санын коюп чыгабыз. Анда мындай болот:

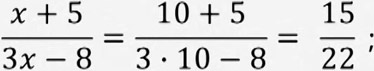
Эгер 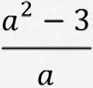бөлчөк берилип "A"нын мааниси -1ге барабар болсо (а=-1), анда бөлчөктөгү "A"лардын ордуна -1 санын коюп чыгабыз:

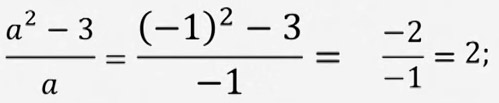
Кийинки деле ушундай, эгер 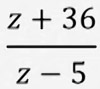бөлчөк берилип "Z" 5ге барабар болсо (z=5), анда бөлчөктөгү "Z"тердин ордуна 5 санын коюп чыгабыз:

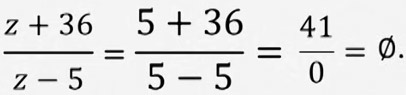
Бул жерден сан нөлгө бөлүнүп жатат, ал эми санды нөлгө бөлүүгө болбойт экенин, барыбыз билебиз.

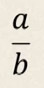- бөлчөк экени белгилүү.

Ал эми алымы жана бөлүмү көп мүчөлөрдөн турган бөлчөк рационалдык бөлчөк деп аталат (рационалдык туюнтма менен алмаштырбайлы).

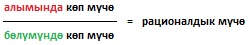
Мисалы,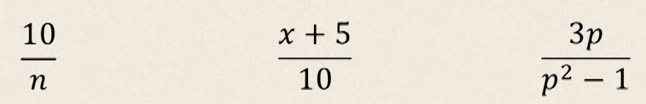

Рационалдык бөлчөктүн аныкталуу областы - бөлүмү нөлгө барабар болбогон өзгөрмөнүн (переменная) бардык маанилери болот.

Төмөнкү рационалдык бөлчөктөрдүн аныкталуу областын көрсөткүлө:

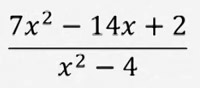
Бардык бөлчөктүн аныкталуу областы x² - 4 = 0, x = 2 жана x = -2 сандарынан башка бардык анык сандардын көптүгү.

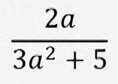
"a"нын бардык маанилеринде 3а² + 5 ≠ 0, берилген бөлчөктүн аныкталуу областы бардык анык сандардын көптүгү.

Теңдештик

Теңдештиктер рационалдык туюнтмаларга байланыштуу болгондуктан эске сала кетели.

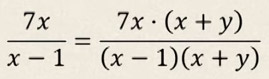
Өзгөрүлмө чоңдуктун берилген бардык маанилеринде барабардык аткарылса теңдештик деп аталат.

Эки туюнтманын маанилери юири-бирине барабар болсо теңдеш барабар деп аталат.

Бир туюнтманы экинчи бир туюнтмага алмаштыруу туюнтманы теңдеш өзгөртүү деп дейбиз.

Эгерде ad = bc, көп мүчөлөрү b ≠ 0 жана d ≠ 0, мында теңдештик ,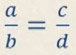

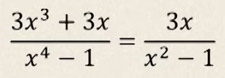
Бул барабардык xтин бардык маанилеринде туура болот, башкача айтканда x = -1 жана x = 1 маанилеринен башка бардык x үчүн туура. Себеби, (3x³ + 3x) (x² - 1) = 3x(x⁴ - 1).

Бөлчөктөрдүн негизги касиеттери

Эгерде бөлчөктүн алымын жана бөлүмүн нөлдөн айырмалуу көп мүчөгө көбөйтсөк ага барабар бөлчөктү алабыз.

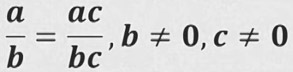
Ушундай эле ыкма менен бөлсөк ага барабар бөлчөккө ээ болобуз.

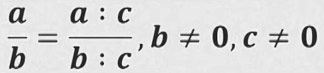
Рационалдык бөлчөктүн негизги касиетин колдонуу менен бөлчөктөрдү кыскартууга жана жаңы бөлүмгө келтирүүгө болот.

Рационалдык бөлчөктү кыскартуу үчүн - бөлчөктүн алымын жана бөлүмүн көбөйтүүчүлөргө ажыратып алып, аны жалпы көбөйтүүчүлөргө бөлүп жиберүү керек.

Бөлчөктү жаңы бөлүмгө келтирүү

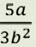бөлчөгүн 21a³b² деген бөлүмгө келтирүү:

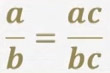- формуласы менен

21a³b² = 3b² * 7a³ анткени, 21ди 3кө бөлсөк 7 чыгат (7a³ - кошумча көп мүчө).

Демек,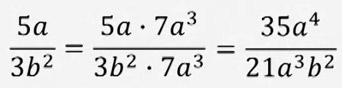

Бөлчөктү кыскартуу

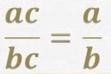- формуласы менен

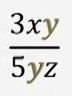- бул жерден "y"терди кыскартып жиберип 5zтен 3x калат.

Бөлүмдөрү бирдей болгон рационалдык бөлчөктөрдү кошуу

Бөлүмдөрү бирдей болгон рационалдык бөлчөктөрдү кошуу үчүн бөлүмүнүн өзүн жазып алымдарын кошуп коебуз.

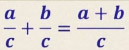- формуласын колдонуу.

a, b жана c - көп мүчөлөр, мында c ≠ 0.

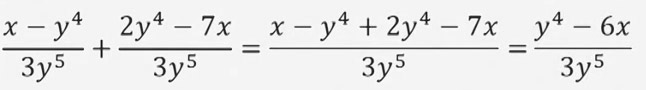
Бөлүмдөрү бирдей болгон рационалдык бөлчөктөрдү кемитүү

Бөлүмдөрү бирдей болгон рационалдык бөлчөктөрдү кемитүү үчүн бөлүмүнүн өзүн жазып алымдарын кемитип коебуз.

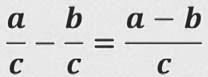- формуласы

a, b жана c - көп мүчөлөр, мында c ≠ 0.

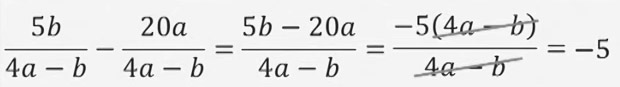
Бөлүмдөрү ар түрдүү болгон рационалдык бөлчөктөрдү кошуу жана кемитүү

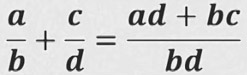- кошуу.

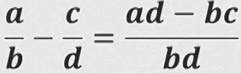- кемитүү.

a, b жана c - көп мүчөлөр, мында b ≠ 0, d ≠ 0.

Бөлчөктөрдү эң кичине жалпы бөлүнүүчүсүнө келтирүүнүн алгоритми:

1. Бөлчөктөрдүн бөлүмүн көп мүчөлөргө ажыратуу;
2. Ар бир бөлчөктүн толуктоочу көбөйтүндүсүн табуу. Ал көбөйтүндү бөлчөктүн бөлүмдөрүндө болбогон көбөйтүндүлөрдөн турат;
3. Ар бир бөлчөктүн алымын жана бөлүмүн анын толуктоочу көбөйтүндүлөрүнө көбөйтүү.

Рационалдык бөлчөктөрдү көбөйтүү

Бөлчөктү бөлчөккө көбөйтүү үчүн, биринчи бөлчөктүн алымын экинчи бөлчөктүн алымына көбөйтүп алымына, биринчи бөлчөктүн бөлүмүн экинчи бөлчөктүн бөлүмүнө көбөйтүп бөлүмүнө жазабыз.

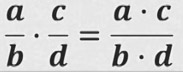- формуласы

a, b, c, d - көп мүчөлөр, мында b ≠ 0, d ≠ 0.

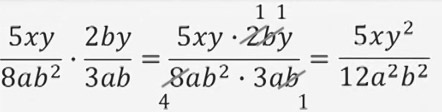
Рационалдык бөлчөктөрдү даражага көтөрүү

Бөлчөктү даражага көтөрүү үчүн бөлчөктүн алымын даражага көтөрүп алымына жазып, бөлүмүн даражага көтөрүп бөлүмүнө жазабыз.

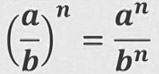- формуласы

a, b, d - көп мүчөлөр, мында b ≠ 0, d ≠ 0.

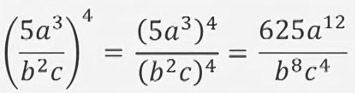
Рационалдык бөлчөктү бөлүү

Бөлчөктү бөлчөккө бөлүү үчүн биринчи бөлчөктүн өзүн жазып, экинчи бөлчөктүн алымы менен бөлүмүн алмаштырып, алымын алымына, бөлүмүн бөлүмүнө көбөйтөбүз.

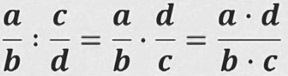- формула

a, b, c, d көп мүчөлөр, мында b ≠ 0, c ≠ 0, d ≠ 0.