Гук закону

Гук закону (гук мыйзамы) — серпилгич нерсеге (пружина, өзөк, консоль, устун ж. б.), жумшалган күчкө пропорцианалдуу пайда болуучу деформация ырастоосу. Же башкача айтканда: сырткы күчтөрдүн таасири астында нерсенин деформацияланышында пайда болгон серпилгич күчү ал нерсенин узарышына түз пропорциялаш болуу ырастоосу. 1660-жылы англис окумуштуусу Роберт Гук тарабынан ачылган.

Деформация — бул сырткы күчтүн таасири астында нерселенин формасынын же көлөмүнүн өзгөрүшү. Акыркы маалымат боюнча нерсе деформацияланышына карата бешке бөлүнөт: кысылуу, ийилүү, чоюлуу (созулуу), жылышуу жана толгонуу (бурулуу, айлануу). Ал эми деформация негизи экиге бөлүнөт: калдыктуу жана калдыксыз. Эгер нерсе дефомацияланган соң, баштапкы абалына келбесе калдыктуу деформация болот. Ал эми деформацияланган соң, алгачкы калыбына келсе, калдыксыз болот.

Гуктун мыйзамы (закону) анча чоң деформацияларда гана аткарыларын эстен чыгарбоо керек. Пропорционалдуулуктун чегинен жогорку болгондо чыңалуу менен деформациянын ортосундагы байланыш түз сызыктуу болбойт калат. Гуктун мыйзамы көптөгөн чөйрөлөр үчүн анча чоң эмес деформацияда дагы колдонууга мүмкүн эмес.

Гуктун пружинага болгон мыйзамы F_s — эркин учун өзүн карай тарткан, пружинага берилген күчтүн кайтып келүүчү күчү деген макулдашуусуна ылайык калыптанган. Мындай учурда теңдеме төмөкүдөй түргөө ээ болот

Пружинага болгон формуласы: F = -kx

Жука нерсе үчүн Гуктун мыйзамы

Жука чоюлуучу нерсе үчүн Гуктун мыйзамы төмөнкүдөй түргө ээ:

F = k Δ l (Δ — дельта)

Мында F — нерсени чоюуучу (кысуучу) күч, Δ l — нерсенин абсолюттук узаруусу (кысылуусу), а k — серпилгичтик коэффициенти (же катуулук).

Серпилгичтик коэффициенти материалдын касиетинен, ошондой эле нерсенин өлчөмүнөн көз каранды.

Нерсенин өлчөмүнөн көз карандылыктарды серпилгичтүүлүк коэффициентин төмөнкүдөй жазып таап алууга мүмкүн (туурасынан кесилиш аянты S жана узундугу L)

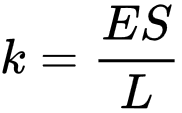
E чоңдугу — биринчи түрдөгү серпилгичтүүлүк модулу (Юнга модулу) аталат, жана материалдык механикалык мүнөздөмөсү болот.

Эгер салыштырмалуу узартууну

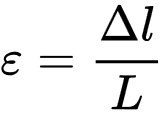
жана туурасынан кесилиш чыңалуусунун нормалдуусун киргизсек, мында ε — эпсилон

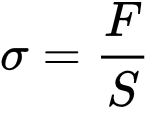
анда салыштырмалуу чоңдуктар үчүн Гук закону төмөнкүдөй жазылат. Мында, σ — сигма — механикалык чыңалуу, S — нерсенин кесилиш аянты.

σ = E ε.

Мындай формада ал каалаган көлөмдөгү материалдарга адилеттүү. Ошондой эле түз нерселерди эсептөөдө Гук мыйзамынын салыштырмалуу формасындагы жазуусун колдонушат

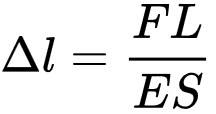
Гуктун жалпылаштырылган мыйзамы

Чыңалуу менен деформациянын жалпы учурунда үч өлчөмдүү мейкиндикте (9 компонентке ээ) экинчи рангдагы тензорлор (латынча tensus, «чыңалган») менен баяндалат.

Аларды байланыштырган туруктуу серпилгичтик тензор, төртүнчү рангдагы C_ijkl тензор болуп, 81 коэффициенткен ээ. Тензордун симметриясынын натыйжасында C_ijkl, ошондой эле чыңалуу жана деформация тензорлордун 21 көз карандысыз туруктуулугу болот. Мында гук мыйзамы төмөнкүдөй болот:

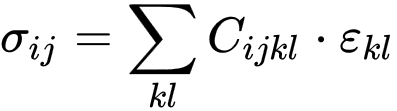
мында σ_ij — чыңалуу тензору, ε_kl, — деформация тензору. Изотроптук материал үчүн C_ijkl тензору эки гана көз карандысыз коэффициентке ээ.

Чыңалуу жана деформация тензорлорунун симметриясына ылайык, Гук закону матрицалык формала берилиши мүмкүн.

Түз сызыктуу серпилгич изотроп нерсеге (телого):

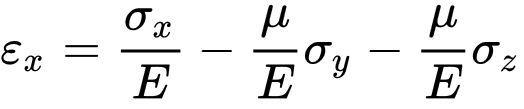
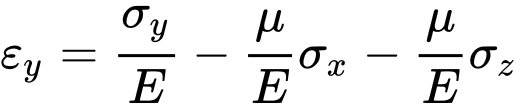
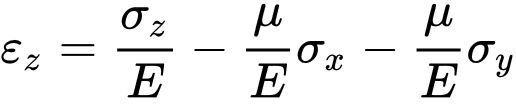
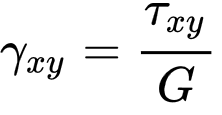
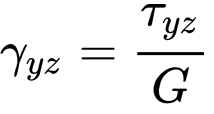
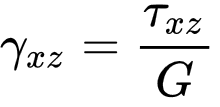
мында:

E — Юнга модулу;
μ — Пуассон коэффициенти;
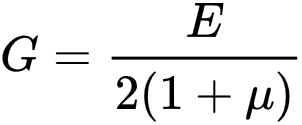— жылышуу модулу.